お久しぶりです。新人のナカノでございます。
トクハラがカタカナ表記なのでこれから私もカタカナで参ります…などと悠長なことを言う前に。
前回の記事から2週間以上経ってしまったことを謝罪いたします。
申し訳ありません!!!
光の速さで移動していたから竜宮城に出張してましたetc…などしょうもない理由を考えたりもしましたが本当に申し訳ありません。
本当は昨日実施された基本情報技術者試験の試験勉強をしてしたのです。
それはまたの機会に。
読者の方には見えないでしょうが土下座をしています。
頭を地面に擦りつけすぎておでこから血が出ています。
また、ブログ読者様のために間を繋いでくださったトクハラさんにも感謝いたします。
では、前回のおさらいを。
ゆとり教育で円周率3が話題になったものの円周率の本質を理解せずに騒いでる人が多いのではないかというお話でした。
そこで東京大学の2003年の問題を紹介したのですが今回はその解説中心の記事になります。
まず円周率は何を意味する数字なのかを理解していないと始まりません。
単刀直入に言って円周率とは円周の長さは直径の何倍ですか?ということです。
先生「問題です、直径1メートルの円の円周は何メートルでしょう?」
生徒「はい、3.14159265359…」
と、なっているのが現在もなお続く円周率計算なのです。
ざっと調べたところ円周率らしきものを確認できる最古のものは紀元前2000年頃の
バビロニア数学が書かれた粘土板 (現在のイランで出土) だそうです。
「昔の人がそんなもん知ってどーすんのー?」とおっしゃられる方もいると思います。
この当時、円周率を何の目的で求めていたのかは流石にわかりません。
そっちの解明は研究者に任せてまだわからないという方のために架空の昔話で考えましょう。
まだ円周率という概念がメジャーでない昔々のある国のお話です。
直径10メートルの塔を建てることになりました。
レンガの横幅は20センチあります。(ここでは計算を簡単にするため厚みを無視します)
塔建設の責任者はレンガがいくつ必要かを計算するのは当然ですよね。
何段積むかは(塔の高さ)÷(レンガの高さ)で計算できます。
問題は1周分です。
円周率を知らない人ですから円周がいくらになるかはわかりません。
実際に並べて確認するくらいしかありません。
小さい円を作ってひもで円周の長さに切って相似で求めるなんてやり方もあるでしょうが・・。
でも(直径10メートル)×(円周率)を使えば1周分に必要なレンガの数は大体求められます。
ではバビロニアだとか昔の人はどうやって円周率を求めていたのか。
円と内接・外接する正多角形の外周との比較がメジャーな方法でした。
この図のように多角形の角の数が増えれば増えるほど外周が円周の長さに近づくことがわかると思います。
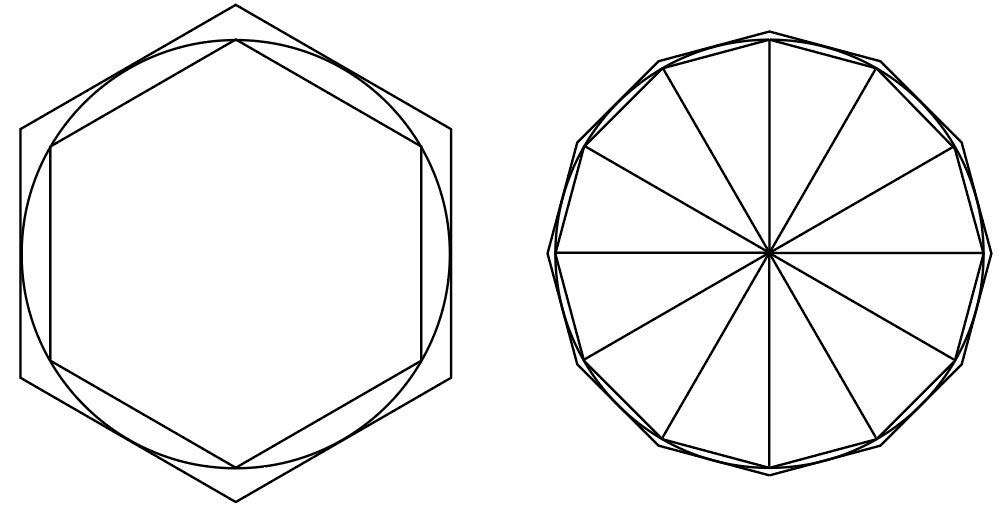
↑↑↑↑↑↑↑ ↑↑↑↑↑↑↑↑
正6角形 正12角形
東大の問題もこれを使って解かせたかったんだと思います。
問題は 3. 05より大きいことを証明すれば良いので円に内接する方だけ考えましょう。
ここからは算数でつまづいた人にわかるような言葉で説明していきます
高校の時に習う
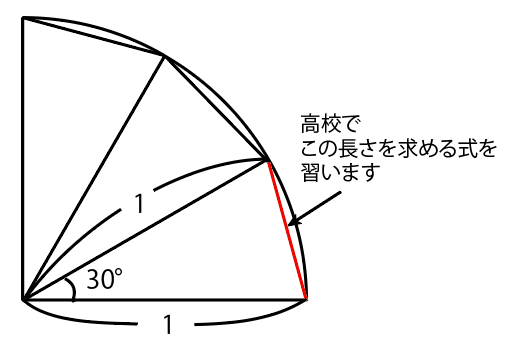
「三角形の二辺だけ長さがわかっている時、その二つの辺が挟んでいる角の大きさがわかれば残りの辺の長さもわかる」という式を使うのです。余弦(よげん)定理という名前です。正12角形を拡大しましょう。
<ここに図が入る>
12角形をケーキを切り分けるように三角形12個で分解すると、一辺の長さがわかります。
円に内接するのでこの辺とこの辺は長さが 1
そしてそれを挟む角は360° ÷ 12 = 30°と大きさがわかるので前述の式を使い、そこで出た値を12倍して長さを出します。
それが 3. 05より大きいことを証明すればいいのです。
他にも(内接する正多角形の面積)<(円の面積)で証明してもOKです。
級数(規則性を持つ数字を足して出た和)で攻めたトリッキーな受験生もいたでしょうね(^_^;)。
話が少しそれました。
何が言いたいかと言うと円周率は単に3.14・・・と覚えて試験で吐き出して点をもらうものではないのです。
円周率は『実用性がある数』つまり『使える数』なんです!
というわけで今回は東京大学 2003年の問題についてお話ししました。
ちゃんとした解き方を知りたい方は「東大 3.05 解法」でググればたくさん出てくるのでそちらでどうぞ。